- 度量对称轴将多边形切割成两份后的对称损失(SIou) L,令切分成两份的多边形面积分别为 S1 和 S2 ,两个面积分别对其余凸包上的点求导。
- L 对多边形上的点 x 坐标求偏导
S2=S−S1
L=(SS1−S2)2=(S2S1−S)2
∂L=2∗S2S1−S∗∂S2S1−S
∂S2S1−S=∂(2SS1−1)=2S2∂S1∗S−∂S∗S1
∂L=4∗S3(2S1−S)∗(∂S1∗S−∂S∗S1)
- 原版 GIoU 损失与梯度推导
- S 表示预测凸包的面积, Sgt 表示真值面积(不会产生梯度), I 表示交集多边形面积, U 表示并集多边形面积
L=UI−CC−U=UI+CU−1
U=S+Sgt−I
∂U=∂S−∂I
∂L=U2(∂I∗U−∂U∗I)+C2∂U∗C−∂C∗U
∂L=U2(∂I∗U−(∂S−∂I)∗I)+C∂S−∂I−C2∂C∗U
- 将两者合并后损失和梯度可以分别表示为
L=GIoU−SIoU
∂L=∂LGIoU−∂LSIoU
- 非独立自变量梯度计算
两个中间变量 + 一个独立变量 §
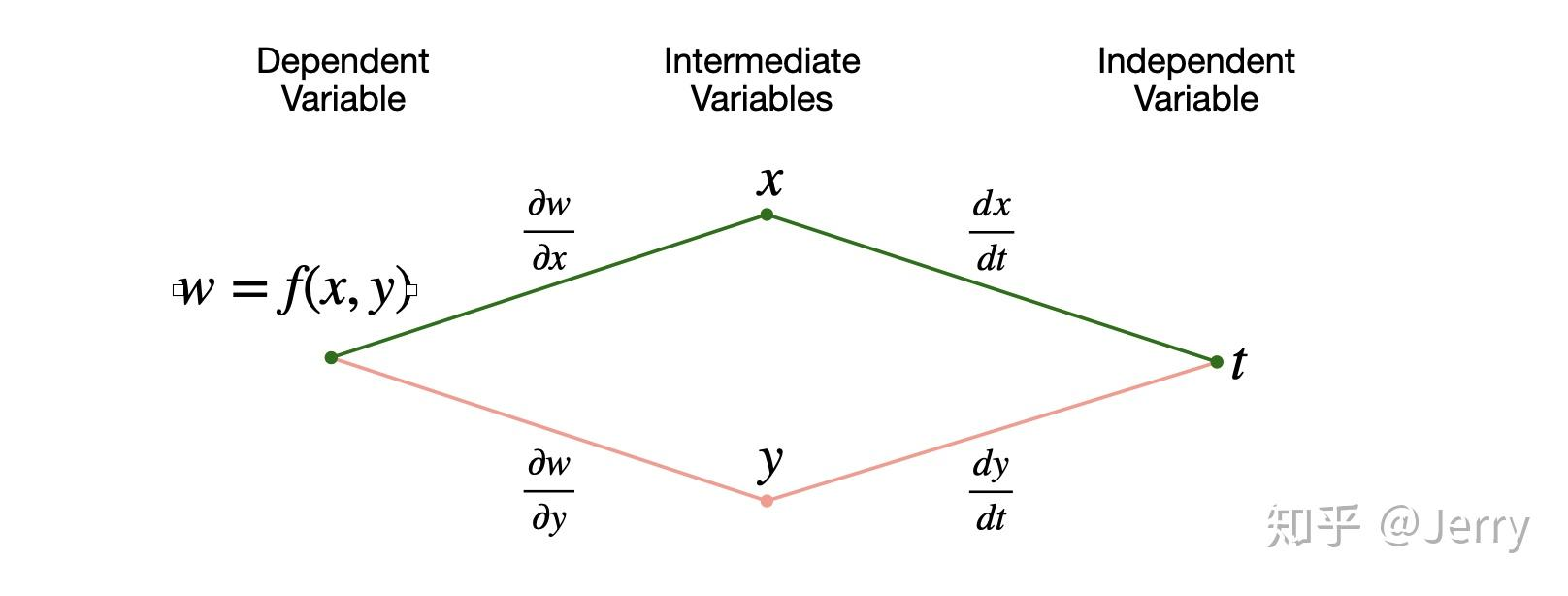
dtdw=∂x∂wdtdx+∂y∂wdtdy
Link to original
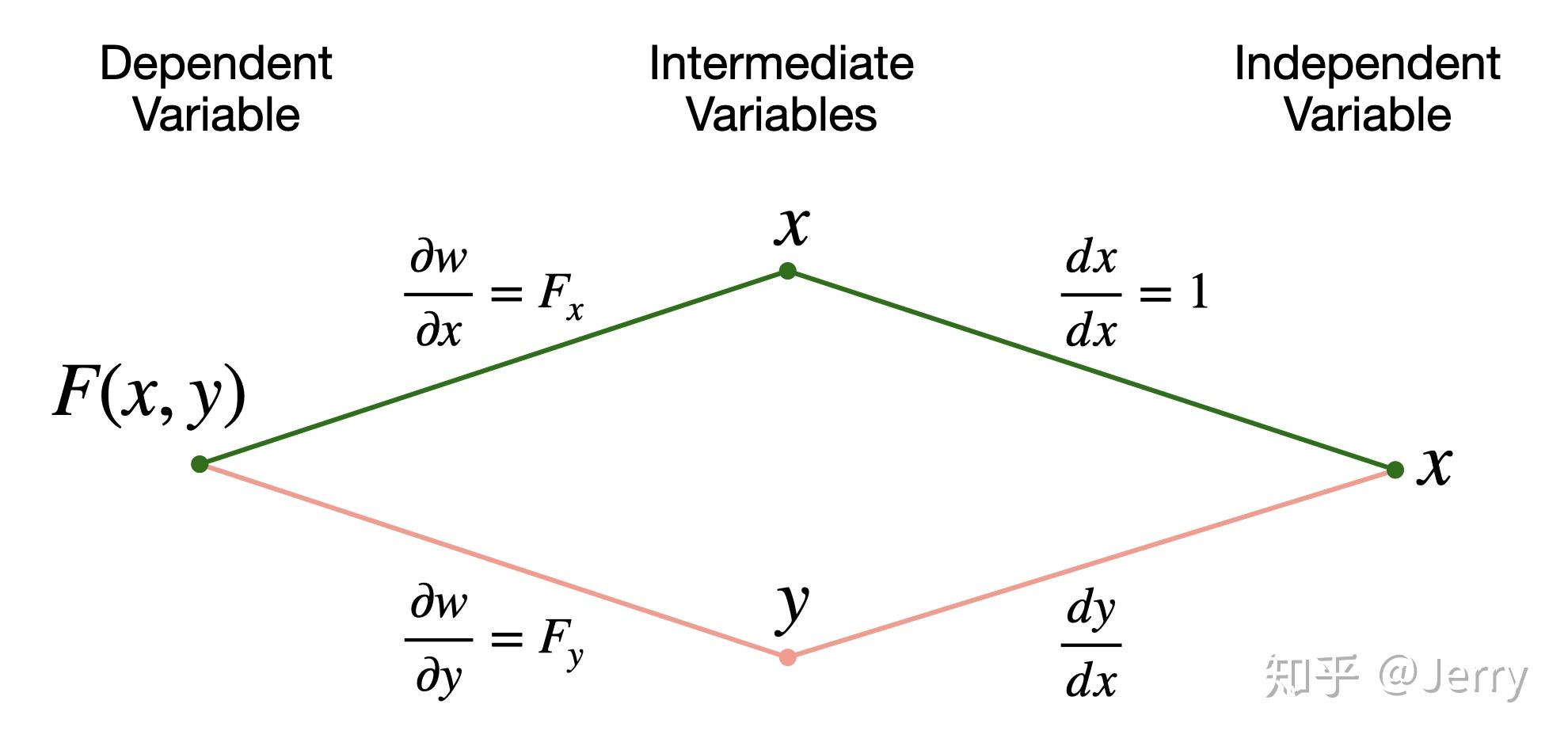 设预测点 P1 对称点 P2=H(P1)
设预测点 P1 对称点 P2=H(P1)
dp1dIoU=∂p1∂IoUdp1dp1+∂p2∂IoUdp1dp2=∂p1∂IoU+∂p2∂IoU⋅dp1dp2
dp1dIoU
 设预测点 对称点
设预测点 对称点  设预测点 对称点
设预测点 对称点