Camera

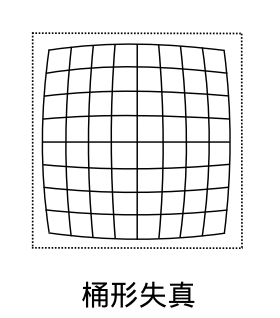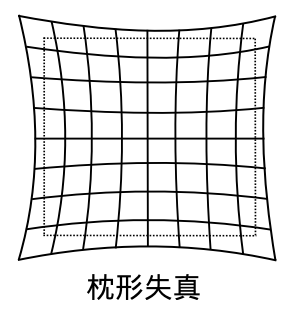
相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程 能够用一个几何模型进行描述。这个模型有很多种，其中最简单的称为针孔模型。

单目相机 §

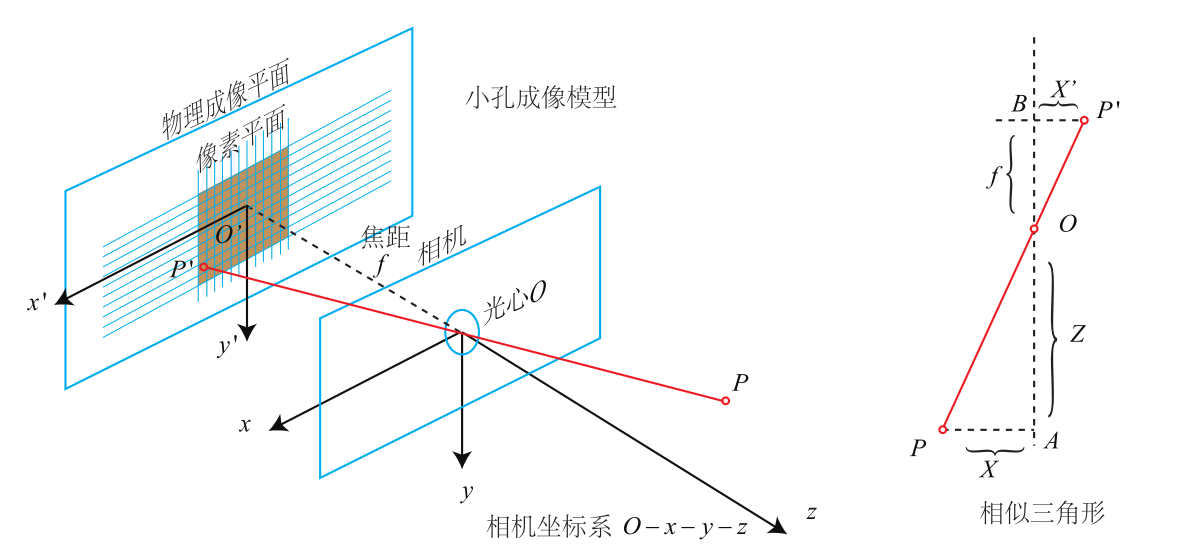
针孔模型 §

$$\frac{Z}{f}=\frac{X}{X^{\prime }}=\frac{Y}{Y^{\prime }}$$ $$\begin{gathered} X^{\prime }=f\frac{X}{Z} \\ {Y}^{\prime }=f\frac{Y}{Z} \end{gathered}$$

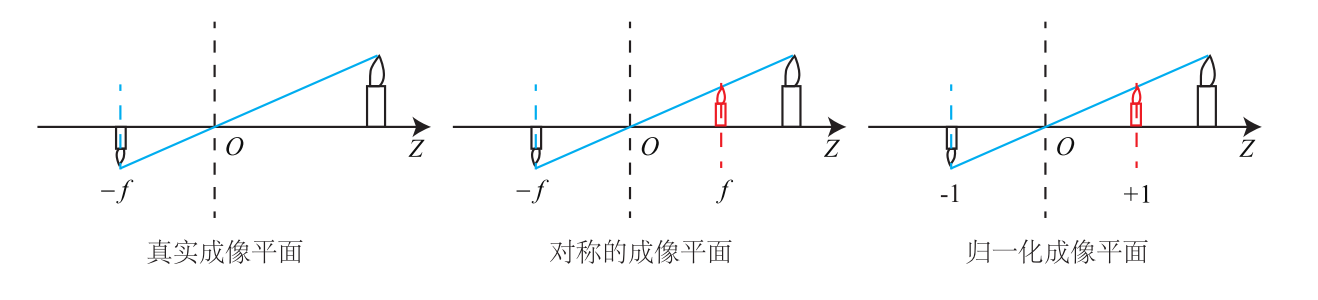
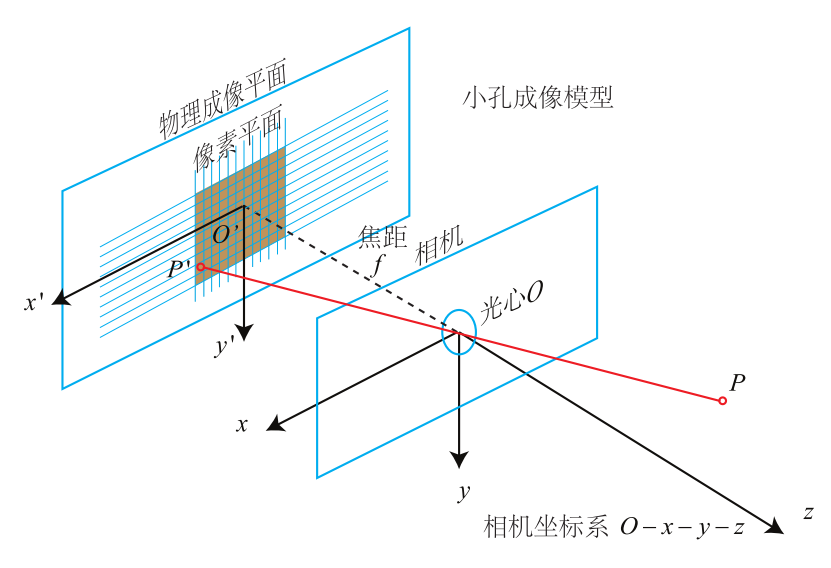
• $f$: 焦距
• $X,Y$: 三维空间相对于光心$O$的坐标(相机坐标系)
• $X^{\prime },Y^{\prime }$: 投影到相对于$O^{\prime }$的坐标

像素坐标系 §

原点 o′ 位于图像的左上角，u 轴向右与 x 轴平行，v轴向下与 y 轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。

设像素坐标在 u 轴上缩放了 α 倍，在 v 上缩放了 β 倍。同时，原点平移了 $[c_x,c_y{]}^T$

$$\{\begin{array}{l}u=\alpha X^{\prime }+c_x\\ v=\beta y^{\prime }+c_y\end{array}$$ $$\{\begin{array}{l}u=f_x\frac{X}{Z}+c_x\\ v=f_y\frac{Y}{Z}+c_y\end{array}$$ $$Z\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)=KP$$

• $K$: 相机内参数矩阵
• $P$: 相机坐标系下的点的坐标

畸变 §

• 径向畸变(穿过图像中心和光轴有交点的直线还能保持形状不变)

  1. 
  2. 

• 切向畸变

  

总结 §

Camera库 §

project_point_radial §

1. 世界坐标系转换到相机坐标系

N = P.shape[0]
X = R.dot(P.T - T)  # rotate and translate

$$P_c=R{P}_w+t$$

2. 归一化

XX = X[:2, :] / X[2, :]  # 2x16

$$P_c=[\frac{X}{Z},\frac{Y}{Z},1{]}^T$$

3. 调整过畸变的相机坐标转像素坐标(物理成像面)

Proj = (f * XXX) + c  # 2x16
Proj = Proj.T

4. 相机坐标的深度

D = X[2, ]

load_camera_params §

1. $R$: 相机旋转矩阵
2. $T$: 相机平移矩阵
3. $f$: 相机焦距长度
4. $c$: 相机中心
5. $k$: 相机径向变形系数
6. $p$: 相机切向变形系数

双目相机 §

基础模型 §

首先这个模型是基于针孔模型的

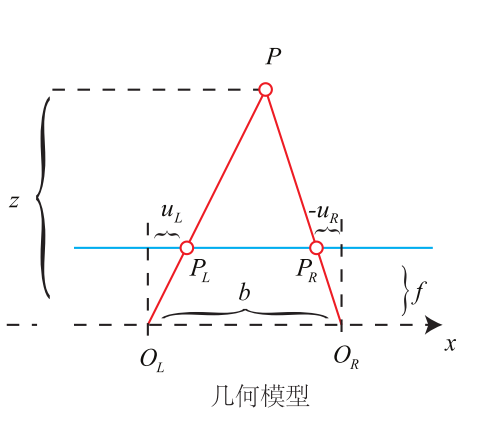
• $u_L,u_R$: 像素坐标
• $O_L,O_R$: 光心
• $b$: 基线
• $z$: 需要求的深度

$$\frac{z-f}{z}=\frac{b-u_L+u_R}{b}$$ $$z=\frac{fb}{d},d=u_L-uR$$

$d$为左右图的横坐标之差，称为视差